Algoritmos de Ruta Más Corta: La Guía Completa de TecnoRynxo

En el corazón de cada GPS, aplicación de mapas, red logística e incluso en el diseño de redes de comunicación, reside un fascinante campo de la informática: los algoritmos de la ruta más corta. Estos poderosos procesos matemáticos son los héroes anónimos que nos permiten navegar el mundo digital y físico con una eficiencia asombrosa. En TecnoRynxo, hemos profundizado en este universo para explicarte no solo qué son, sino también para desglosar los algoritmas más populares y los más innovadores que están definiendo el futuro.

El problema es simple de plantear: dado un conjunto de puntos conectados (un grafo), ¿cuál es el camino más eficiente para ir de un punto A a un punto B? La "eficiencia" puede medirse en distancia, tiempo, costo o cualquier otra métrica. Resolver esto es crucial para innumerables tecnologías que usamos a diario.

Los Clásicos: Pilares de la Búsqueda de Caminos

Existen algoritmos que, por su robustez y genialidad, se han convertido en los pilares fundamentales sobre los que se construye toda la teoría de búsqueda de rutas. Conocerlos es entender la base de la navegación moderna.

Algoritmo de Dijkstra: El Pionero Confiable

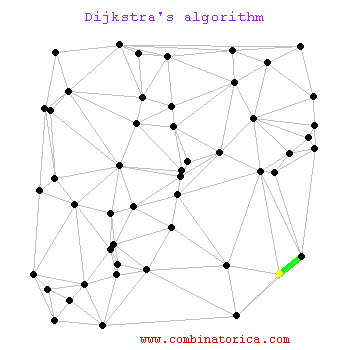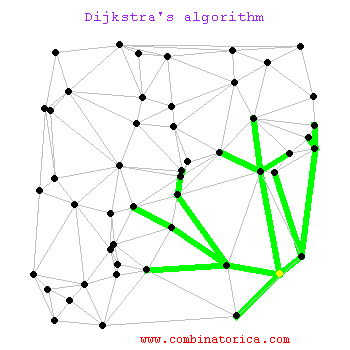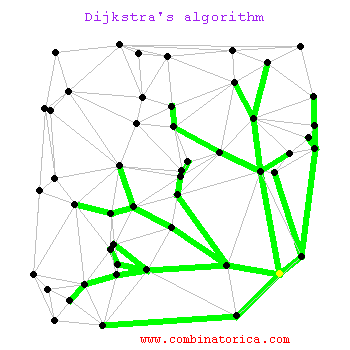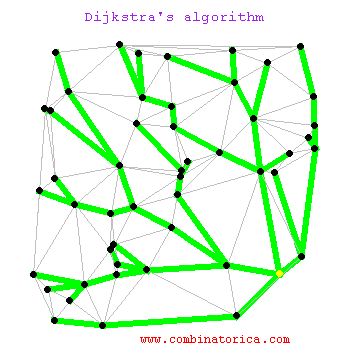
Creado por Edsger W. Dijkstra en 1956, este es a menudo el primer algoritmo que se aprende y por una buena razón. El Algoritmo de Dijkstra es excepcionalmente bueno para encontrar el camino más corto desde un único punto de origen hacia todos los demás puntos en un grafo donde las conexiones (aristas) tienen un "peso" o "costo" no negativo.

¿Cómo funciona? Dijkstra opera de manera metódica y expansiva.

1. Comienza en el nodo de origen, al que le asigna una distancia de 0.
2. Explora los nodos vecinos, calculando la distancia desde el origen hasta ellos.
3. Selecciona el nodo no visitado con la distancia más corta y lo marca como "visitado".
4. Repite el proceso, actualizando las distancias de los vecinos si encuentra una ruta más corta a través del nodo recién visitado.

Es como una mancha de aceite que se expande uniformemente en todas direcciones hasta encontrar su objetivo. Su principal limitación es que no funciona si hay pesos negativos (por ejemplo, una ruta que te "paga" por usarla), pero para la mayoría de las aplicaciones del mundo real, como las redes de carreteras, es una base sólida y eficiente.

Algoritmo A* (A-Estrella): La Búsqueda Inteligente

Si Dijkstra es un explorador metódico, A* es un explorador con un mapa y una brújula. Es una evolución de Dijkstra que introduce una "heurística": una estimación inteligente de cuán lejos está un nodo del destino final.

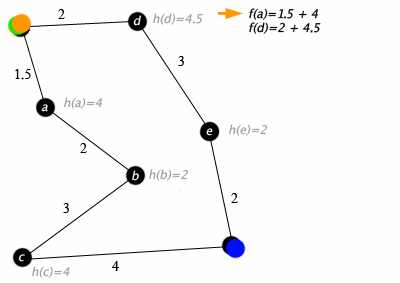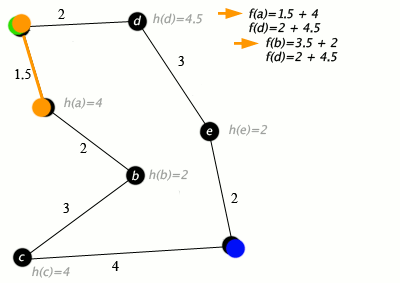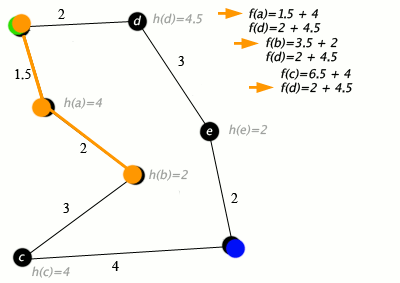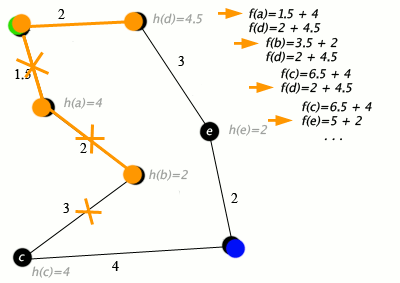
¿Cómo funciona? A* combina dos métricas para decidir qué nodo explorar a continuación:

• g(n): El costo real del camino desde el nodo de inicio hasta el nodo actual (lo mismo que usa Dijkstra).
• h(n): El costo estimado (heurístico) desde el nodo actual hasta el nodo destino.

Al sumar ambas (f(n) = g(n) + h(n)), A* prioriza los caminos que no solo son cortos hasta ahora, sino que también parecen prometedores para llegar al destino. Esto evita que el algoritmo explore en direcciones obviamente incorrectas, haciéndolo significativamente más rápido que Dijkstra en grafos grandes, como los de los videojuegos o la robótica. Nuestra experiencia nos muestra que para aplicaciones en tiempo real, A* suele ser la opción preferida sobre Dijkstra.

Algoritmo de Bellman-Ford: El Especialista en Pesos Negativos

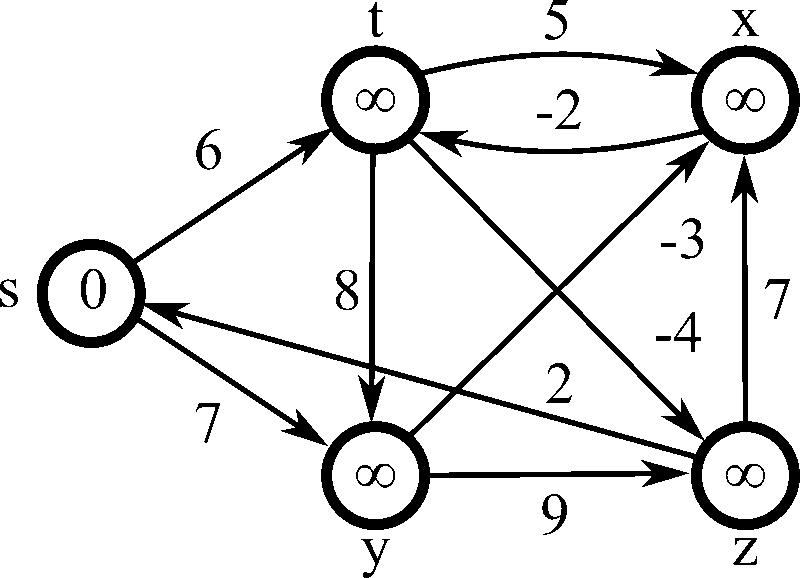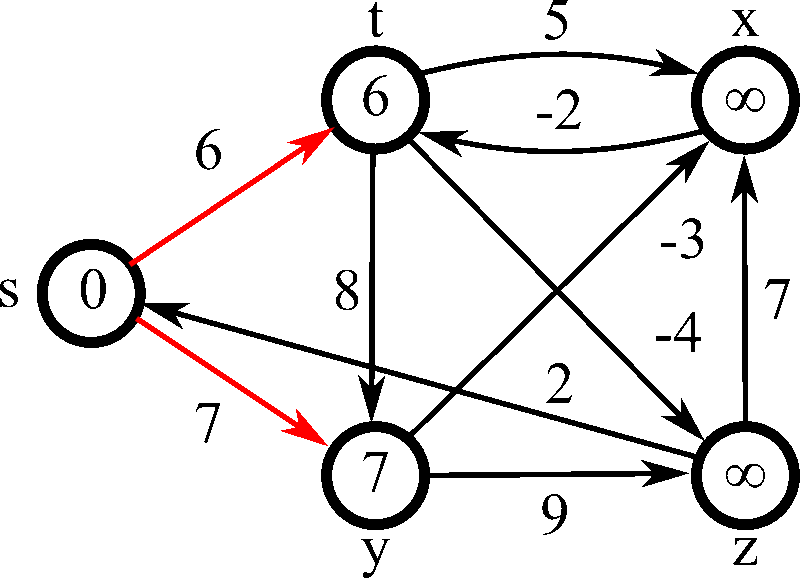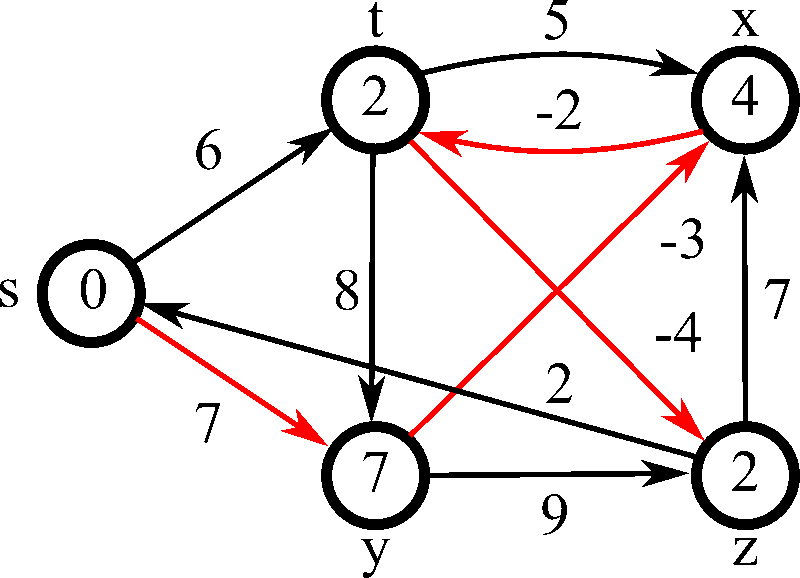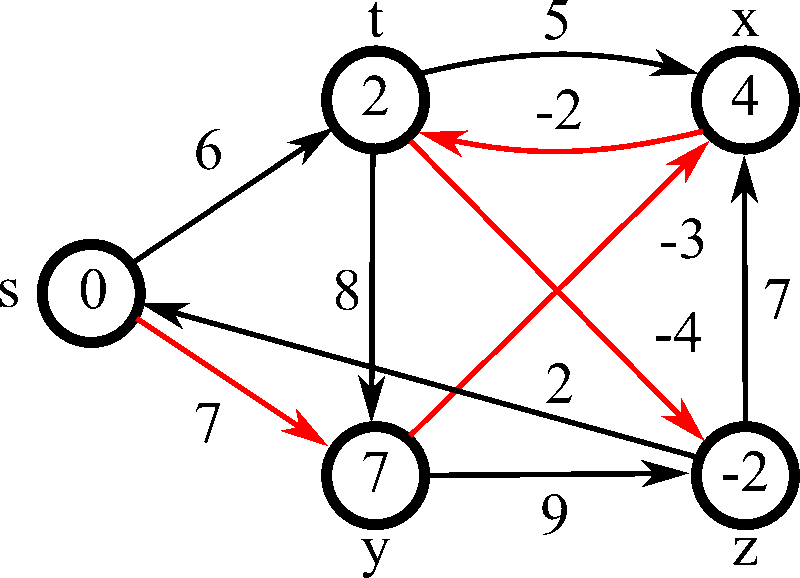
¿Qué pasa cuando las reglas del juego cambian y algunas rutas pueden tener un costo negativo? Aquí es donde Dijkstra falla y el Algoritmo de Bellman-Ford brilla. Aunque es más lento que Dijkstra, su capacidad para manejar aristas con pesos negativos lo hace indispensable en campos como las finanzas y el arbitraje de redes.

La gran ventaja de Bellman-Ford es que también puede detectar "ciclos negativos", un escenario donde se puede recorrer un bucle indefinidamente para reducir el costo total a menos infinito. El algoritmo funciona "relajando" todas las aristas del grafo repetidamente, garantizando que después de un número determinado de iteraciones, se ha encontrado la distancia más corta, o se ha detectado un ciclo imposible.

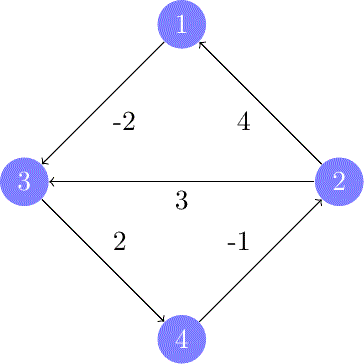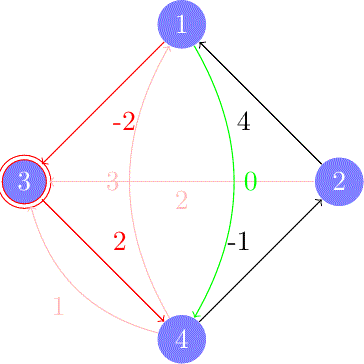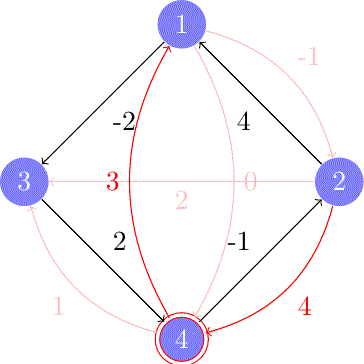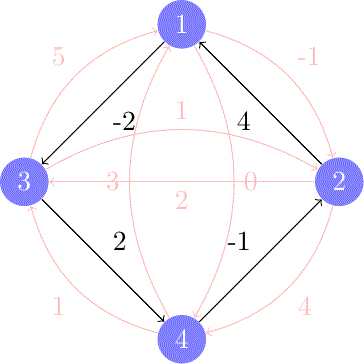
Algoritmo de Floyd-Warshall: La Solución "Todos con Todos"

Mientras que los algoritmos anteriores se centran en encontrar la ruta desde un único punto de origen, el Algoritmo de Floyd-Warshall aborda un problema mucho más ambicioso: encontrar la ruta más corta entre todos los pares de nodos en un grafo.

Utiliza programación dinámica para construir la solución de manera incremental. Itera a través de todos los nodos y considera a cada uno como un punto intermedio en un camino. Es increíblemente potente para análisis de redes densas donde se necesita conocer la conectividad global, como en el análisis de redes sociales o la planificación de infraestructuras.

Las Nuevas Fronteras: Velocidad para el Mundo Moderno

Los mapas de hoy en día contienen millones de nodos. Ejecutar Dijkstra o A* en un grafo de esa escala para una consulta en tiempo real sería demasiado lento. Por eso, han surgido algoritmos más nuevos que utilizan una fase de "preprocesamiento" para acelerar las consultas de manera espectacular.

Contraction Hierarchies (CH)

Esta es una de las técnicas más exitosas utilizadas en sistemas de navegación como Google Maps. La idea central de las Contraction Hierarchies es crear una "autopista" virtual en el grafo.

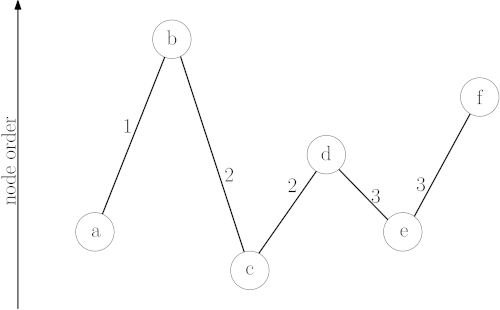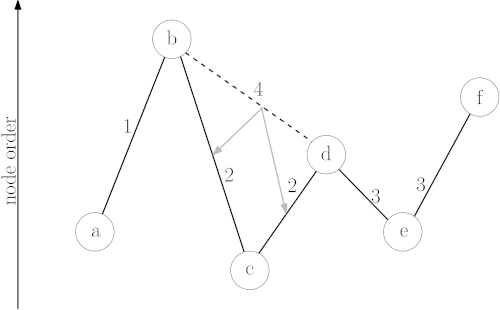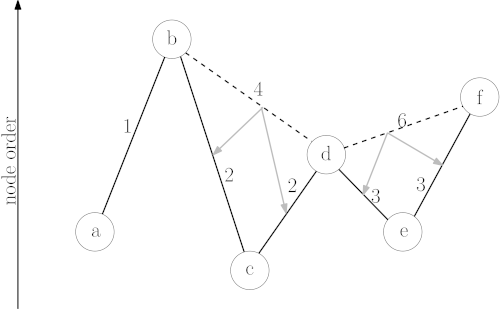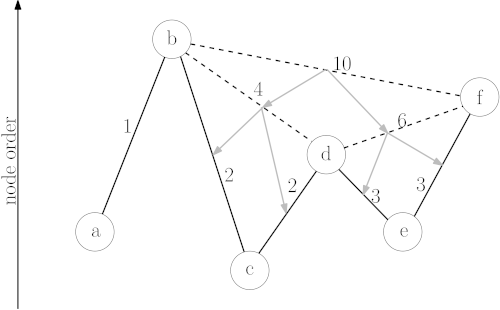
Durante la fase de preprocesamiento, los nodos se ordenan por importancia (por ejemplo, una intersección en una autopista principal es más importante que una en una calle residencial). Luego, el algoritmo "contrae" los nodos menos importantes, creando atajos que representan las rutas más rápidas a través de ellos. Cuando se realiza una consulta, la búsqueda se dirige rápidamente hacia arriba en la jerarquía de nodos importantes, encuentra un camino a través de la "red de autopistas" y luego desciende hacia el destino. Esto reduce drásticamente el número de nodos que deben explorarse.

insertar imagen de un grafo con nodos de diferentes tamaños para representar la jerarquía

Transit Node Routing (TNR)

El Transit Node Routing lleva la idea de las autopistas un paso más allá. Se basa en la observación de que cuando viajas una larga distancia, casi siempre pasas por un conjunto relativamente pequeño de puntos de transferencia o "nodos de tránsito".

El preprocesamiento identifica estos nodos de tránsito y calcula las distancias entre todos ellos. Para encontrar una ruta entre dos puntos, el algoritmo solo necesita:

1. Identificar los nodos de tránsito más cercanos al origen (sus "nodos de acceso").
2. Identificar los nodos de tránsito más cercanos al destino.
3. Consultar las distancias precalculadas entre estos conjuntos de nodos de tránsito para encontrar la mejor combinación.

Este método puede responder consultas a escala continental en microsegundos, ya que la búsqueda se reduce a unas pocas búsquedas en tablas precalculadas.

Aplicaciones Prácticas: Más Allá de los Mapas

Aunque la navegación es el ejemplo más obvio, estos algoritmos son omnipresentes:

• Redes de Computadoras: Protocolos como OSPF (Open Shortest Path First) utilizan el algoritmo de Dijkstra para enrutar el tráfico de datos a través de Internet de la manera más eficiente.
• Logística y Cadena de Suministro: Optimizan las rutas de entrega para empresas de paquetería y transporte, ahorrando tiempo y combustible.
• Inteligencia Artificial y Videojuegos: El algoritmo A* es fundamental para que los personajes no jugadores (NPCs) naveguen por los mundos virtuales de forma realista.
• Biología y Genómica: Se utilizan para encontrar similitudes y relaciones en las complejas redes de interacciones de proteínas o secuencias genéticas.

FAQ: Preguntas Frecuentes sobre Algoritmos de Ruta

¿Cuál es el algoritmo de la ruta más corta más rápido?

No hay una única respuesta. Para grafos de tamaño moderado sin pesos negativos, Dijkstra es muy eficiente. Para grafos grandes donde se conoce la dirección del objetivo (como en mapas), A* suele ser más rápido. Para consultas extremadamente rápidas en redes viales a gran escala, algoritmos con preprocesamiento como Contraction Hierarchies son los reyes indiscutibles.

¿Puede un algoritmo de ruta más corta usar datos en tiempo real, como el tráfico?

Sí. Los grafos pueden ser dinámicos. Sistemas como Google Maps o Waze actualizan constantemente los "pesos" de las aristas (las carreteras) en función de los datos del tráfico en tiempo real. Un camino que era el más corto hace cinco minutos puede no serlo ahora, y los algoritmos se ejecutan de nuevo para encontrar la nueva ruta óptima.

¿Dijkstra y A siempre encuentran la ruta más corta?

Sí, con una condición. Dijkstra garantiza encontrar la ruta más corta siempre que no haya pesos de arista negativos. A* también garantiza la ruta óptima siempre que su función heurística sea "admisible", lo que significa que nunca sobreestima el costo real para llegar al destino.

Conclusión: La Continua Evolución de Encontrar el Mejor Camino

Desde el metódico Dijkstra hasta las ultrarrápidas Contraction Hierarchies, los algoritmos de la ruta más corta han transformado nuestra capacidad para modelar y navegar sistemas complejos. Lo que comenzó como un problema teórico de la teoría de grafos es ahora una tecnología fundamental que impulsa la eficiencia en casi todas las industrias. En TecnoRynxo, seguiremos atentos a las innovaciones en este campo, porque encontrar el camino más corto es, en esencia, una búsqueda constante de la solución más inteligente.